Topics Covered in this DOPE GUIDE
Manhattan distance
Euclidean distance
Minkowski distance
Pearson Correlation Coefficient
Cosine similarity
Implementing k-nearest neighbors in Python
Now to get into some real cool stuff, familia

A Data Mining Expert
So what is Collaborative Filtering, anyway, other than “just a data mining technique”?
A recommendation system wherein I collaborate with friends to filter out your online information for pertinent data and then use it to stalk your movements online. JKJKJKJKJKJKJK LMAO!!!
Collaborative Filtering is a recommendation system where I use people with similar interests to recommend some sort of data, like a movie. In this way, the data points in your set “collaborate” to produce some sort of prediction. Suppose I need to recommend you an album to listen to on Spotify: I would go through the other users on Spotify to find one that is similar to you in music tastes. Once I find this person, I can look at music that they listen to that you don’t and recommend you those artists.
The following guide will go over some of those oh-so-sweet details on how this process works.
BUT HOW DO WE MEASURE SIMILARITY BASED-GOD MAXWELL?
Manhattan Distance
Imagine yourself and Harambe the gorilla, rating your preferences on different movies. Harambe, of course, rates Free Willy a 10/10 and rates Pulp Fiction a solid 8/10. You, on the other hand, rate Pulp Fiction a solid 10/10, and Free Willy a 3/10. What is the simplest manner in which we can measure your similarity to this majestic primitive? Distance. We would plot your opinions on Free Willy on the x axis, and your opinions on Pulp Fiction on the y axis, and then calculate how many blocks a cab driver in matthattan would have to move in order to get from Harambe to You.
| x1 - x2| + | y1 - y2 |
| 10 - 3 | + | 8 - 10 | = 9
And so your manhattan distance from dank memes is a 9. Now lets talk about Rare Pepe’s. Pepe rates Free Will a 0/10, and feels meh about Pulp Fiction, rating it a 7/10. His manhattan distance from you is therefore
| 3 - 0 | + | 10 - 7 | = 6
Thus you are closer to Pepe than you are to Harambe. This is the simplest form of measuring similarity
Euclidean Distance and the Illuminati
So, everyone knows that the Illuminati are watching our every move, and to perfect the measure of similarity, they forced Pythagoras to churn out the Famous triangular theorem, creating the concept of Euclidean Distance. You will hopefully have learned this in high school and I will be killed if I tell you more, but it is pretty straight forward that measuring the exact distance between two points will give you a slightly more accurate representation of similarity. Here’s the equation:
sqrt( (x1 - x2)^2 + (y1 - y2)^2 )
WE NEED TO GO DEEPER.
DEEPER.
WE MUST GO DEEPER INTO HIGHER DIMENSIONS.
Thinking of how the concepts of Manhattan Distance and Euclidean Distance apply when we have ratings of more than one movie is relatively straight-forward. Instead of just x and y coordinates, we have x, y, and z, coordinates, a 3-D distance, and with four movies, we have x, y, z, and theta coordinates, and so forth. The associated measures of distance change intuitively.
Manhattan Distance becomes | x1 - x2 | + | y1 - y2 | + | z1 - z2 | + …
Euclidean Distance becomes sqrt( (x1 - x2)^2 + (y1 - y2)^2 + (z1 - z2)^2 + … )
And boom, you’re a space explorer mathmatician extrodinate working in 5 dimensional space. E. Z. P. Z. MIND FREKING BLOWN GAME OVER SHOW DONE WE”RE OUT OF HERE. BEAUTIFUL. AMAZING. 10/10 BEST NEW MATHEMATICAL CONCEPT.
BUT WHAT IS WRONG WITH THIS PICTURE?
WAIT, NO, NOT THE PICTURE ABOVE. WHAT IS WRONG WITH THE METHODS OF CALCULATING EUCLIDEAN AND MANHATTAN DISTANCE?
This one is a little bit harder to explain without giving a specific example. Imagine trying to apply these measurements of similarity when there are a large number of ratings. Users will have incredibly different overlaps. I might have rated 5 movies, and Harambe has rated the same five, while Pepe has rated two of the ones that I’ve rated and 3 movies that I have never seen. Now, when we try to draw a comparison between me, harambe, and Pepe, there may be a large skew in the results. My distance to harambe may be larger simply because of the larger number of dimensions between us, even if in reality we are closer. This, as well as many other problems, can arise. Bad news, and it is actively being researched as we speak. We will talk more about this later, hopefully, and adress ways in which his bias may be corrected. For now, let us discuss the generalized distance measurement (its really freaking cool, though the math is a little less intuitive.)
NEVER PANIC
Math is not for geniuses. Everything is generally understandable given enough time and experience. So don’t panic. Good Will Hunting is a lie. Still, we will take it slow, but I promise that nothing in the following sections, and the rest of this book, will go unexplained.
Now let’s get to the good stuff, the Minkowski Distance Metric, this big boy.
Note: If you have not encountered the notation above for dealing with series, heres a quick and easy explanation: YouTube. .
So let’s break it down. When p = 1, we have the manhattan distance:
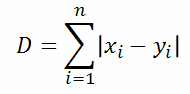
And when p = 2, we’ve got Euclidean:
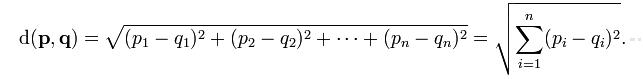
And so we get a rough idea of what this formula is communicating.
DISTANCE. IT REVEALS A FUNDAMENTAL TRUTH ABOUT THE MEASUREMENT OF DISTANCE IN TWO DIMENSIONAL SPACE. THIS EQUATION, MINKOWSKI DISTANCE, GIVEN DIFFERENT P VALUES, REVEALS DIFFERENT POSSIBLE MEASURES OF DISTANCE, EACH OF WHICH WEIGHS THE IMPORTANCE OF THE RATIO BETWEEN X AN Y VALUES DIFFERENTLY. SOUNDS AND SEEMS COMPLICATED, BUT THE EASIEST WAY TO THINK ABOUT IT FOR MYSELF IS THAT IT IS JUST A FUNCTION THAT WILL RETURN TO YOU A DIFFERENT WAY TO MEASURE DISTANCE GIVEN DIFFERENT INPUTS. P COOL RIGHT? MATH IS BEAUTIFUL. JUST, LIKE, THIS THING, THESE COUPLE OF SYMBOLS, CONDENSE LITERALLY AN INFINITE NUMBER OF DIFFERENT WAYS TO MEASURE DISTANCE IN TWO DIMENSIONAL SPACE. HERES A PICTURE OF THESE WAYS, DEPICTED AS SHAPES, SEE HOW THE CIRCLE IS EUCLIDEAN WHEREAS THE DIAMOND IS MANHATTAN? THIS IS BECAUSE THE MEASURE OF DISTANCE IN MANHATTAN TERMS IS “TRIANGULAR”, A SIMPLE ADDITION OF THE SUMS, WHEREAS THE MEASURE IN EUCLIDEAN TERMS RELIES UPON THE SQUARE ROOT OF THE SUM OF THE SQUARES, E.G. “CIRCULAR”. IT IS KIND OF FUNNY TO TALK ABOUT AND IM NOT SURE THE BEST WAY TO GO ABOUT IT, BUT HOPEFULLY YOU KIND OF GET WHAT I MEAN. AT THE VERY LEAST TODAY YOU LEARNED ABOUT MINKOWSKI DISTANCE WHICH MAY OR MAY NOT BE IMPORTANT TO YOU OR YOUR FUTURE EMPLOYMENT, BUT WHO CARES LMAO? MATH IS GREAT AND THAT’S WHAT REALLY COUNTS.

Getting back to the topic at hand. Distance is important, especially for Data Science, as, if we want to recommend a good book to Miles Jones, our best bet is most likely to look for the person most similar to Miles, in terms of distance, and recommend a book that this “closest neighbor” liked that Miles Jones has not read.
Time for the Pearson Correlation Coefficient, otherwise known as the thing I tell literally everyone about when they ask me about Data Science.
CAPS LOCK IS CRUISE CONTROL FOR COOL.
So people are different, and rate things differently. I might rate things on a scale of 1 to 10, whereas Harambe might only rate them on a scale of 4 to 5. So things aren’t objective. How do data scientists deal with this “grade inflation?” As with anything dank, there is a math equation. The Pearson Correlation Coefficient describes the similarity of two people for whom the grading scale is subjective. It is pretty sick, but before I get into it, lets get into some dank memes.



That’s good, now let’s get into some real stuff familia. The Pearson Correlation Coefficient:
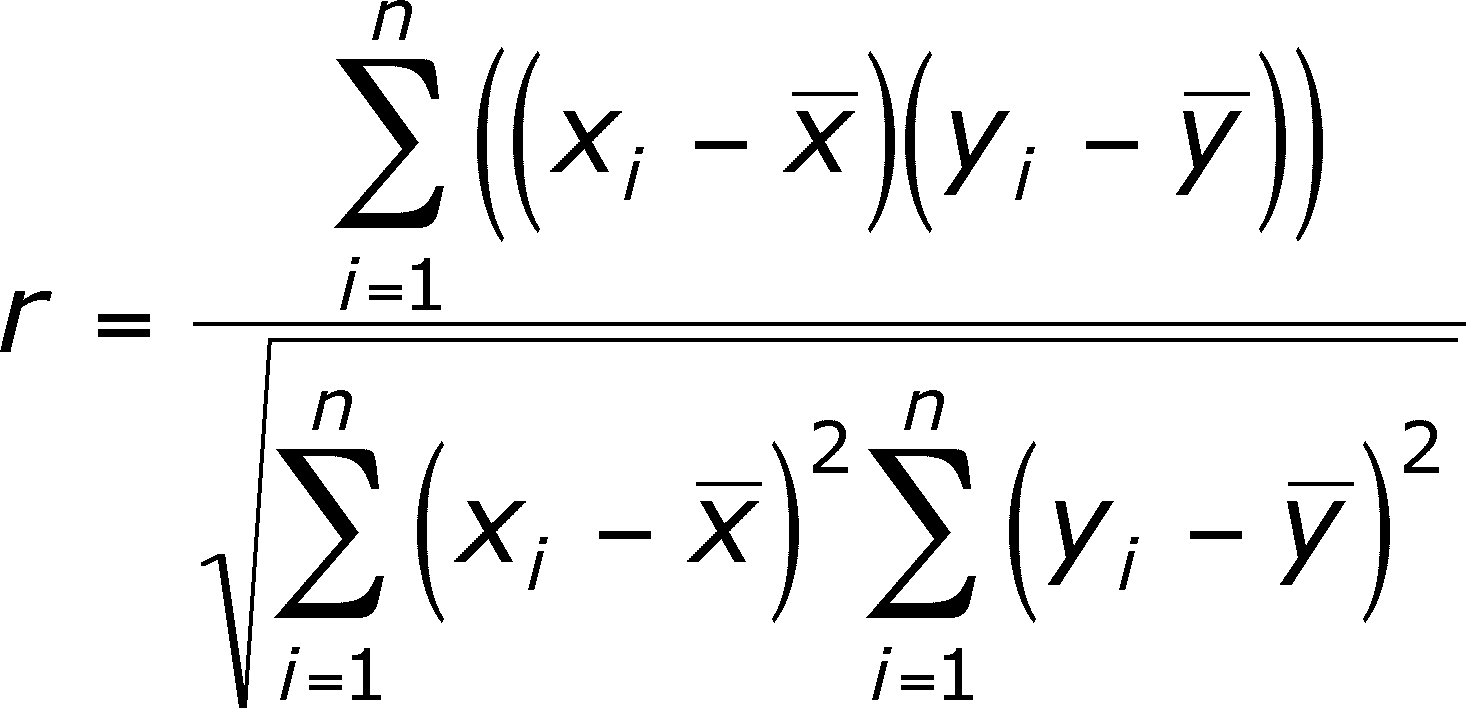
This equation will pop out a number betweeen -1 and 1, with 0 being no correlation between two people’s subjective ratings and 1 being a really high correlation. Negative one is a really high correlation of disagreement. Simply put, if I rate this on a scale of 4 and 5, whereas you rate things on a scale from one to five, we can be in really good agreement, even if our scales are different, really good disagreement, or not really compatible measurements. This, of course, allows us to make measures of similarity even with skewed data.
HOWEVER, THE EQUATION ABOVE IS REALLY A PAIN TO COMPUTE, SO WE WILL USE THIS ONE INSTEAD.
LMAOOOOOOOO!!!
Kay, don’t be scared. We’re going to walk through what this means. But then again, I’m v lazy so I’m going to steal an explanation from another book, and then explain “why” it works.
